Analysis of Planetary Gearsets - Advanced

On the preceding page, I demonstrated a simple, tabular method for calculating speeds in a planetary gearset with one input fixed. This was mainly intended to help build your intuition for these fascinating systems. We now turn our attention to developing a more general method for analyzing planetary gearsets. One of the downsides to the tabular method shown on the previous page is that it is challenging to calculate speeds when both inputs are moving - that is, with no fixed input.

In order to model the hybrid powertrain, we would also prefer a set of algebraic expressions, rather than a set of tables. While it is possible to use a 'lookup table' in Simulink, we will find it much easier to use an algebraic formula in our model.

To begin the analysis, imagine for the moment that we hold the carrier fixed. Define the basic ratio, b, as

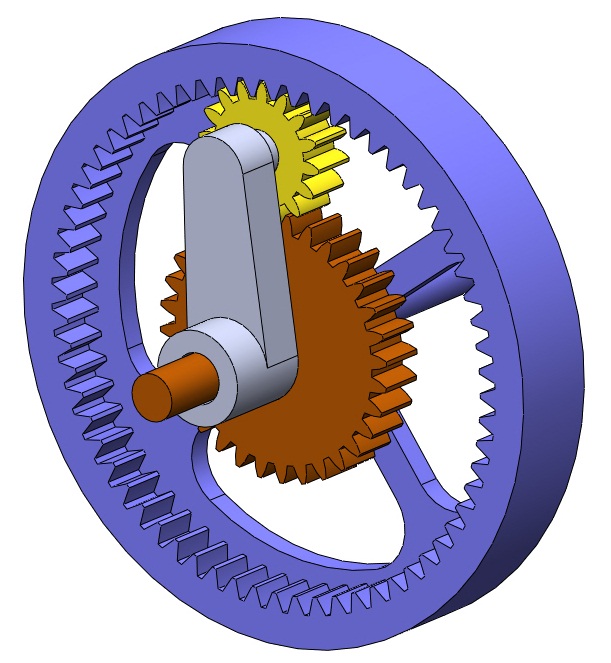
$$b= \frac{\text{speed of faster input shaft}}{\text{speed of slower input shaft}} \text{ (with the carrier held fixed)}$$

As an example, consider the gearset shown above. Let us assume that the sun gear has $N_s = 32$, the planet has $N_p = 16$ and the ring has $N_r = 64$. As an initial guess, let us suppose that the sun gear spins faster than the ring gear. Hold the carrier fixed and give the ring one revolution. The planet turns

$$n_p=\frac{N_r}{N_p}n_r=\frac{64}{16}(1\text{ rev})=4\text{ rev}$$

or 4 revolutions. The sign preceding the gear ratio is positive because the ring gear is internal (the ring and planet revolve in the same direction). If the planet gear makes 4 revolutions, the sun gear makes

$$n_s=-\frac{N_p}{N_s}n_p=\frac{16}{32}(4\text{ rev})=-2\text{ rev}$$

Thus, for every 1 revolution of the ring, the sun makes -2 revolutions. The basic ratio is then

$$b=-2$$

While it is possible for the basic ratio to be positive or negative, its magnitude must always be greater than or equal to 1, since we have defined it as the ratio of the faster speed to the slower. Thus

$$|b|\ge1$$

by definition. The efficiency formulas on a later page will not work if b is less than 1.

In the preceding analysis we held the carrier fixed, but the relationship between the input and output gears must hold no matter what the carrier does. That is, rotation of the carrier (and orbiting of the planets) does not affect the ratio between sun and ring, since this ratio is determined by the numbers of teeth in each gear.

Let us now repeat the preceding analysis, but this time allow the carrier to rotate. Define $\phi_f$ as the number of rotations that the faster gear rotates relative to the carrier. That is

$$\phi_f=n_f-n_c$$

where $n_f$ and $n_c$ give the number of rotations (relative to ground) of the faster gear and carrier, respectively. Also, define $\phi_s$ as the number of rotations that the slower gear makes relative to the carrier

$$\phi_s=n_s-n_c$$

Since the speed ratio of the two gears must remain even if the carrier rotates, we can write

$$b=\frac{\phi_f}{\phi_s}=\frac{n_f-n_c}{n_s-n_c}$$

Rearrange the equation above to obtain

$$n_f-n_c-b(n_s-n_c)=0$$

Now differentiate this equation to obtain angular velocities

$$\omega_f-\omega_c-b(\omega_s-\omega_c)=0$$

This is the general kinematic equation for a planetary gearset. We can use it to find the speed ratios for any planetary gearset, provided we have obtained the basic ratio in advance. If we know the speeds of the two input shafts, we can use the equation to solve for the output speed. The three equations below give the speed of one gear (or carrier) as a function of the two.

\begin{equation} \omega_f=\omega_c(1-b)+b\omega_s \end{equation} \begin{equation} \omega_s=\frac{1}{b}[\omega_f+\omega_c(b-1)] \end{equation} \begin{equation} \omega_c=\frac{\omega_f-b\omega_s}{1-b} \end{equation}

Example

In the geartrain for the preceding example, let the ring be fixed, and the arm free to move. Find the speed of the arm if the sun moves at 100rpm cw.

Answer

For this example, the ring is the slow gear, and has speed $\omega_s=0\text{ rpm}$. The basic ratio is still -2. Thus, using Equation 3

$$\omega_c=\frac{\omega_f-b\omega_s}{1-b}$$ $$\omega_c=\frac{100-0}{1-(-2)}=\frac{100}{3}=33.3\text{ rpm}$$

or 33.3 rpm cw.

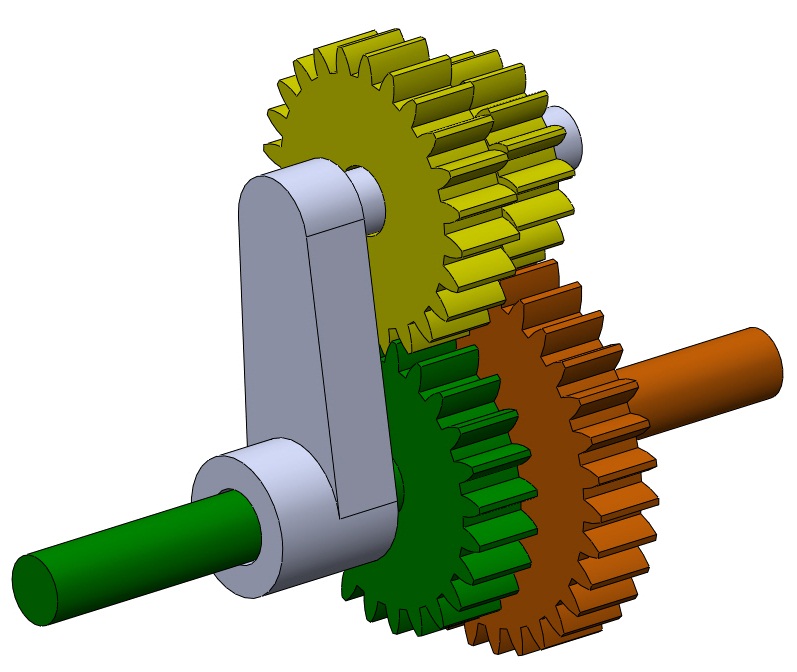
Example: Two Suns, Two Planets

In the planetary gearset shown at right, the first sun (the green gear) has 24 teeth. The second sun (the orange gear) has 32 teeth. The planet meshing with the first sun has 24 teeth and the other planet has 16 teeth. Let us assume that the larger sun (the orange gear) is fixed and the smaller sun (the green gear) is spinning clockwise at 100rpm. How fast does the arm rotate?

Answer

To solve this problem, we must first find the basic ratio. As a guess, let us assume that the small sun is the fast gear and the large sun is the slow gear. Pretend the arm is fixed and rotate the large sun one revolution cw.

$$n_{p1}=-\frac{N_{s1}}{N_{p1}}n_{s1}=-\frac{32}{16}(1\text{ rev})=-2\text{ rev}$$

The two planets are attached to the same shaft, so they experience the same number of rotations.

$$n_{p2}=n_{p1}=-2\text{ rev}$$

Finally, the second sun rotates

$$n_{s2}=-\frac{N_{p2}}{N_{s2}}n_{p2}=-\frac{24}{24}(-2\text{rev})=2\text{ rev}$$

Thus, the basic ratio is

$$b=\frac{n_{s2}}{n_{s1}}=2$$

Now solve for the speed of the carrier using Equation 3. As before, the slow gear is fixed (0 rpm) and the fast gear is spinning at 100 rpm

$$\omega_c=\frac{\omega_f-b\omega_s}{1-b}$$ $$\omega_c=\frac{100-0}{1-2}=\frac{100}{-1}=-100\text{ rpm}$$

or 100 rpm ccw

Example: Two Suns, Two Planets, Revisited

Let us use the same gearset as before (shown in the figure at right) but let the larger sun (the orange gear) be the input spinning at 100rpm cw and hold the smaller sun fixed. What is the speed of the carrier?

Answer

Since we defined the basic ratio assuming that the large sun is the slow gear and the small sun is the fast, $\omega_f$ still applies to the small sun and $\omega_s$ applies to the large sun, despite the fact that the small sun is fixed in this example.

$$\omega_c=\frac{\omega_f-b\omega_s}{1-b}$$ $$\omega_c=\frac{0-2(100)}{1-2}=\frac{-200}{-1}=200\text{ rpm}$$

or 200 rpm cw. It is interesting to note that the arm moves opposite the input in one configuration and in the same direction as the input in the other configuration. This is an example of the counterintuitive behavior of planetary gearsets!

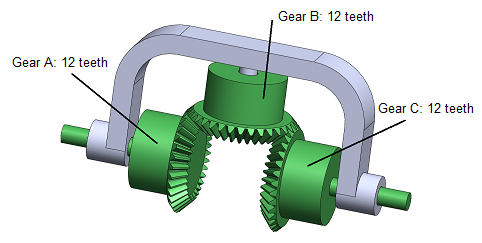
Example: The Differential

In the differential shown above $N_A=N_B=N_C=$ 12 teeth. The inputs are through the shafts attached to gears A and C and the output is the speed of the carrier. What is the speed of the carrier as a function of the two inputs?

Answer

To find the basic ratio let us hold the carrier fixed, and rotate gear A one revolution. Since the number of teeth in each miter gear is the same, gear C will rotate -1 revolution for every revolution of gear A. Thus, the basic ratio is

$$b=-1$$

Since its magnitude is 1, there really is no 'fast' or 'slow' gear – they move with the same speed. We can arbitrarily choose gear A as the 'fast' gear and gear C as the 'slow' gear.

\begin{align*} \omega_c&=\frac{\omega_f-b\omega_s}{1-b}\\ \omega_c&=\frac{\omega_A-(-1)\omega_C}{1-(-1)}\\ \omega_c&=\frac{\omega_A+\omega_C}{2} \end{align*}

The carrier moves at the average speed of the two inputs! If we arrange the inputs such that they turn in opposite directions, the carrier speed will be one-half the difference between the two inputs, hence the name differential. For example, if we wish two large electric motors to have the same speed, we can use the output of a differential to provide a feedback as to their difference.