Efficiency of Planetary Gearsets

The topic of geartrain efficiency has been much studied in the past 100 years, and no simple, all-encompassing theory has emerged. For the purposes of our analysis, it is sufficient to estimate efficiency using the methods of Merritt [1], although many other methods are available. It is common to calculate the power lost in the meshing of two gears as

\begin{equation*} P_{out}=E_0 \cdot P_{in} \end{equation*}

where P_in is the power input into the gear pair, P_out is the power available to be transmitted "downstream" and E₀ is called the "basic efficiency". Most of the power is lost in the gear pair through the rubbing (friction) of the gear teeth as the motion is transmitted, although some is also lost due to friction in the bearings. The efficiency of a pair of gears can be calculated as

$$E_0=1-L$$

where L is the power loss, as estimated in the chart shown below. The chart gives an initial estimate of the power loss in a given gear pair, and the rules given in the next section (described by Molian [2]) can help to refine this estimate.

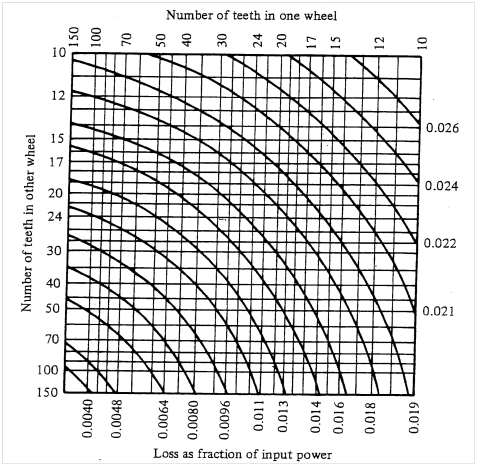
If a geartrain is composed of more than one pair, the efficiencies of both pairs are multiplied to obtain the overall efficiency. Thus, for a compound geartrain with two pairs, the overall efficiency is

$$E_0=E_1 E_2$$ $$E_0=(1-L_1)(1-L_2)$$

Expanding this equation gives

$$E_0=1-L_1-L_2+L_1L_2$$

As seen in the chart, the losses for any individual gear pair are very small, usually on the order of 2% or less. Thus, the term L₁L₂ (which is on the order of 0.0004) is usually negligible relative to the other loss terms (on the order of 0.02) and we may safely omit it. Thus, a good approximation for the efficiency of a compound geartrain is

$$E_0=1-L_1-L_2-...-L_n$$

According to Molian, a few simple rules suffice to approximate the efficiency of a compound geartrain.

	Rules for Calculating Power Loss of a Pair of Spur Gears
1	For external spur gears take the values for L from the table above
2	For an internal spur gear mated with an external spur gear, modify the value of L by the following equation $$L_{int}=\frac{R-1}{R+1} L_{ext}$$ where R is the number of teeth in the large gear divided by the number of teeth in the small gear.
3	For helical gears the value of L given by the chart must be multiplied by 0.8 cos λ, whereλ is the spiral angle. If one of the helical gears is internal, we must modify L as in Rule 2, above.
4	For bevel gears the number of teeth in each wheel must be multiplied by sec θ, where θ is the pitch-cone angle. These new values for the numbers of teeth are used in the chart to find L.

Looking at Rule 2 in the table above we see that an internal gear pair will have lower losses than an external pair, if the gear ratio, R, is small. This is the reason that planetary gearsets commonly use internal gears in their design.

Example 1

Calculate the efficiency of an external spur gear pair where the pinion has 16 teeth and the gear has 32 teeth. Repeat the calculation if the 32-tooth gear is internal.

Answer

Examining the chart above, we see that the power loss for the external gear pair is 0.018, or 1.8%. For the internal pair we have R = 2, so that \begin{align*} L_{int}&=\frac{R-1}{R+1} L_{ext}\\ L_{int}&=\frac{2-1}{2+1} 0.018\\ L_{int}&=0.006 \end{align*}

The losses for the internal gearset are 1/3 of that of the external gearset!

Planetary Gearset Efficiency

The section above provided a means of approximating the efficiency of the spur gears themselves; we now turn our attention to finding the overall efficiency of the planetary gearset. The method we will use is explained thoroughly by Molian [2], I will adopt a slightlymodified explanation here, which I believe is a little clearer.

The first step in calculating the overall efficiency is (as before) to hold the arm fixed, and calculate the basic efficiency, E₀ of the gearset. This basic efficiency must be modified to account for motion of the arm. As we will see, it is possible to design a planetary gearset with a higher efficiency than E₀, although it is also possible to design a planetary gearset with such a low efficiency as to make it useless!

Absolute vs. Relative Velocities

We begin by noting that all power losses due to friction occur because of motion relative to the arm in the gearset; that is, frictional losses can only occur when gear teeth are rubbing against each other. If we were to rotate the entire gearset as a rigid unit, the power loss would be zero, since the gear teeth would not be coming into and out of mesh with each other. Thus, let us define two new angular velocity variables:

\begin{equation} \beta_f=\omega_f-\omega_a\\ \end{equation} \begin{equation} \beta_s=\omega_s-\omega_a\\ \end{equation}

These are the angular velocities of shaft f and shaft s relative to the arm. Power losses due to friction can only occur when these are nonzero. Rotating the entire gearset as a rigid body would make

$$\omega_f=\omega_s=\omega_a$$

which would make

$$\beta_f=\beta_s=0$$

Thus, all frictional power losses are proportional to the relative angular velocities, β_f and β_s, and not the absolute angular velocities, ω_f, ω_s and ω_a.

Power Balance in the Planetary Gearset

We will now derive the power balance equation for the planetary gearset. We will ultimately use this equation (along with a few others) to derive the expressions for efficiency. Recall that the power transmitted by a shaft is the product of torque and angular velocity

$$P=T\omega$$

To begin the derivation, add the torques coming into the gearbox:

\begin{equation} T_f+T_s+T_a=0\\ \end{equation}

In the expression above, it is clear that not all torques can be positive (or negative). If the torque on a shaft has the same sign as its angular velocity, then we infer that the shaft is being driven, usually by a motor. Conversely, if the torque has the opposite sign as the angular velocity, we assume that the shaft is driving a load.

Torque & velocity have same sign → Power > 0 → Shaft is driven by motor
Torque & velocity have opposite sign → Power < 0 → Shaft is driving a load

Conservation of energy dictates that the power leaving the gearbox must be the same as that entering the gearbox (for the moment assuming 100% efficiency.)

\begin{equation} P_f+P_s+P_a=0\\ \end{equation}

Substitute torque and angular velocity for each shaft:

\begin{equation} T_f\omega_f+T_s\omega_s+T_a\omega_a=0\\ \end{equation}

But power losses are only proportional to the relative angular velocities, so substitute the expressions in Equations 1 and 2 to obtain

$$T_f(\beta_f+\omega_a)+T_s(\beta_s+\omega_a)+T_a\omega_a=0$$

rearrange slightly

$$T_f\beta_f+T_s\beta_s+(T_f+T_s+T_a)\omega_a=0$$

but the sum of all three torques is zero, as shown in equation (3) thus

\begin{equation} T_f\beta_f+T_s\beta_s=0\\ \end{equation}

The first term in the expression above is the power consumed by the faster shaft, and the second gives the power consumed by the slower shaft. Up to now we have assumed 100% efficiency in the geartrain. To make the analysis realistic, we must define two cases:

Power enters through the fast shaft $E_0T_f\beta_f+T_s\beta_s=0$
Power enters through the slow shaft $T_f\beta_f+E_0T_s\beta_s=0$

In each expression, only a fraction of the power from the driving shaft is available to the driven shaft.

Example 2: Efficiency of Simple Planetary Gearset

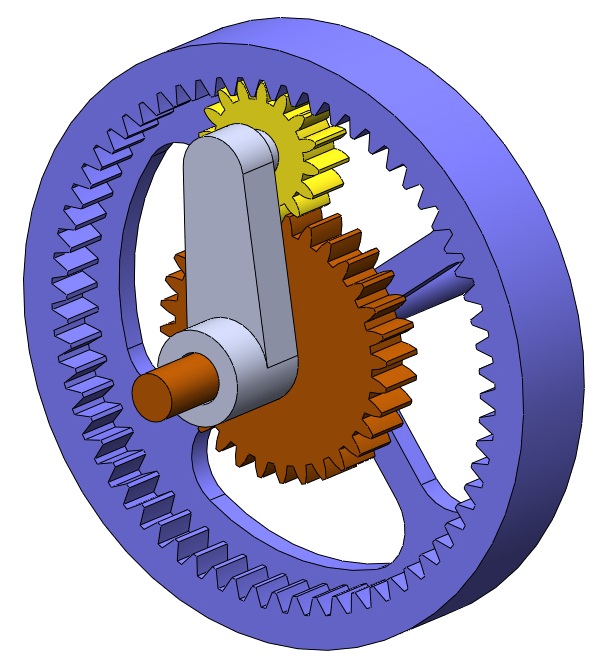
Let us revisit the simple planetary gearset shown in the figure at right. Recall that the sun gear has 32 teeth, the planet has 16 and the ring has 64. We determined earlier that the faster gear is the sun and the slower gear is the ring, and the basic ratio is

$$b=-2$$

Assume that the basic efficiency of the sun/planet/ring is 95%, and that the sun gear is being driven at 100rpm cw, with a load of 50 lbf-in applied to the ring. In this example, the arm is held fixed. How much power is required to drive the sun gear?

Answer

Since the arm is held fixed, we have

$$\beta_f=\omega_f$$ $$\beta_s=\omega_s$$

Power enters through the sun (fast) gear and is transmitted to the ring (slow) gear, so we can use the first of the efficiency expressions above

$$E_0T_f\beta_f+T_s\beta_s=0$$

$$E_0T_f\omega_f+T_s\omega_s=0$$

Solving for the power driving the fast gear gives

$$P_f=T_f\omega_f=-\frac{T_s\omega_s}{E_0}$$

If the sun gear spins at 100rpm cw, the ring gear will spin at

$$\omega_s=\frac{\omega_f}{b}=\frac{100}{-2}=-50\text{rpm}$$

Since the torque on the ring gear is a load, we assume that it acts in the opposite sense that the ring gear is spinning. Thus

$$T_s=50\text{lbf} \cdot \text{in}$$

Substituting this into the power expression above gives

$$P_f=-\frac{\omega_sT_s}{E_0}=275.6\frac{\text{lbf} \cdot \text{in}}{\text{sec}}$$

This example was fairly straightforward, since (with the arm fixed) the gearset behaves as an ordinary, non-epicyclic gearset. In the next example, we will allow the arm to rotate.

Example 3: Efficiency of the Simple Planetary Gearset

For this example, let the input be the sun gear, the output be the arm, and let the ring be fixed. The load on the arm is 50 lbf-in and the sun spins at 100rpm. If the basic efficiency is 95%, what is the efficiency of the planetary gearset in driving the load?

Answer

As before, the "fast" gear is the sun gear and "slow" gear is the ring. Before beginning, it is helpful to assess the known and unknown quantities in this problem:

Known: $T_a, E_0, b, \omega_s=\omega_{ring}, \omega_f=\omega_{sun}$
Unknown: $T_f = T_{sun}, T_s = T_{ring}, \omega_a$

The definition of overall efficiency is

$$E=\left|{\frac{P_{out}}{P_{in}}}\right|=\left|{\frac{T_{out}\omega_{out}}{T_{in}\omega_{in}}}\right| =\left|{\frac{T_a\omega_a}{T_f\omega_f}}\right|$$

where, in this case, the input is the sun gear and the output is the arm. First, let us find the speed of the arm, using the basic kinematic equation for the planetary gearset

$$\omega_a=\frac{\omega_f-b\omega_s}{1-b}$$

where

$$\omega_s = 0\text{rpm}$$ $$\omega_f = 100\text{rpm}$$ $$\omega_a = \frac{100-0}{1-(-2)}=33.33\text{rpm}$$

Since the load torque must have the opposite sign as the shaft speed, we take

$$T_a=-50\text{lbf} \cdot \text{in}$$

The power consumed in driving the load with the arm is

$$P_{out}=T_a\omega_a=-174.51\frac{\text{lbf} \cdot \text{in}}{\text{sec}}$$

To calculate power loss in the gearset, we use the efficiency expression given in case 1

$$E_0T_f\beta_f+T_s\beta_s=0$$ $$\beta_f=\omega_f-\omega_a=100-33.33=66.66\text{rpm}$$ $$\beta_s=\omega_s-\omega_a=0-33.33=-33.33\text{rpm}$$

We still don't know the torque on the ring or the sun, but we can use the fact that the torques must sum to zero to find an expression for T_s.

$$T_s=-T_f-T_a$$

Substituting this into the efficiency expression and solving for T_f gives

$$T_f=\frac{T_a\beta_s}{E_0\beta_f-\beta_s}=\frac{-50\cdot(-33.33)}{0.95\cdot66.66-(-33.33)}=17.24\text{lbf} \cdot\text{in}$$

The overall efficiency is then

$$E=\left|\frac{T_a\omega_a}{T_f\omega_f}\right|=\left|\frac{-50\cdot33.33}{17.24\cdot100}\right|=96.7\%$$

A More General Procedure

The procedure outlined above is tedious and prone to error, and can be simplified considerably by combining the formulas we derived earlier into two tables, as shown below. The first table lists the overall ratios, torques, and efficiencies for the case where the basic ratio is greater than 1, and the second gives the same quantities for basic ratio less than -1. In all cases, the input shaft is defined as the one where torque and speed have the same sign, and the output shaft is the one where torque and speed have opposite sign.

Table 1: Efficiencies where basic ratio is positive. Overall ratio is defined as (input speed)/(output speed).
Case	Input Shaft	Fixed Shaft	Output Shaft	Overall Ratio	T_f	T_s	T_a	Efficiency
1	Fast	Slow	Arm	$$1-b$$	$$\frac{1}{bE_0-1}T_a$$	$$\frac{bE_0}{1-bE_0}T_a$$	$$T_a$$	$$\frac{bE_0-1}{b-1}$$
1	Fast	Arm	Slow	$$b$$	$$-\frac{1}{E_0b}T_s$$	$$T_s$$	$$\frac{1-E_0b}{E_0b}T_s$$	$$E_0$$
2	Slow	Fast	Arm	$$\frac{b-1}{b}$$	$$\frac{1}{bE_0-1}T_a$$	$$\frac{bE_0}{1-bE_0}T_a$$	$$T_a$$	$$\frac{bE_0-1}{E_0(b-1)}$$
2	Slow	Arm	Fast	$$\frac{1}{b}$$	$$T_f$$	$$-\frac{b}{E_0}T_f$$	$$\frac{b-E_0}{E0}T_f$$	$$E_0$$
3	Arm	Fast	Slow	$$\frac{b}{b-1}$$	$$-\frac{E_0}{b}T_s$$	$$T_s$$	$$\frac{E_0-b}{b}T_s$$	$$\frac{b-1}{b-E_0}$$
4	Arm	Slow	Fast	$$\frac{1}{1-b}$$	$$T_f$$	$$-\frac{b}{E_0}T_f$$	$$\frac{b-E_0}{E_0}T_f$$	$$\frac{E_0(b-1)}{b-E_0}$$

Table 2: Efficiencies where basic ratio is negative. Overall ratio is defined as (input speed)/(output speed).
Case	Input Shaft	Fixed Shaft	Output Shaft	Overall Ratio	T_f	T_s	T_a	Efficiency
1	Fast	Slow	Arm	$$1-b$$	$$\frac{1}{bE_0-1}T_a$$	$$\frac{bE_0}{1-bE_0}T_a$$	$$T_a$$	$$\frac{bE_0-1}{b-1}$$
1	Fast	Arm	Slow	$$b$$	$$-\frac{1}{E_0b}T_s$$	$$T_s$$	$$\frac{1-E_0b}{E_0b}T_s$$	$$E_0$$
2	Slow	Fast	Arm	$$\frac{b-1}{b}$$	$$\frac{E_0}{b-1}T_a$$	$$\frac{b}{E_0-b}T_a$$	$$T_a$$	$$\frac{b-E_0}{b-1}$$
2	Slow	Arm	Fast	$$\frac{1}{b}$$	$$T_f$$	$$-\frac{b}{E_0}T_f$$	$$\frac{b-E_0}{E_0}T_f$$	$$E_0$$
3	Arm	Fast	Slow	$$\frac{b}{b-1}$$	$$-\frac{1}{bE_0}T_s$$	$$T_s$$	$$\frac{1-bE_0}{bE_0}T_s$$	$$\frac{E_0(b-1)}{bE_0-1}$$
4	Arm	Slow	Fast	$$\frac{1}{1-b}$$	$$T_f$$	$$-\frac{b}{E_0}T_f$$	$$\frac{b-E_0}{E_0}T_f$$	$$\frac{E_0(b-1)}{b-E_0}$$

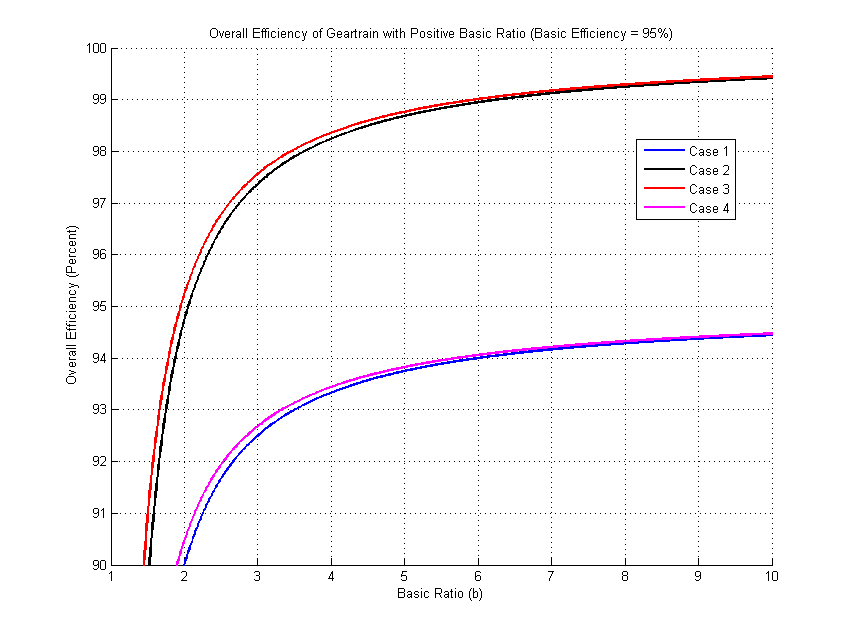
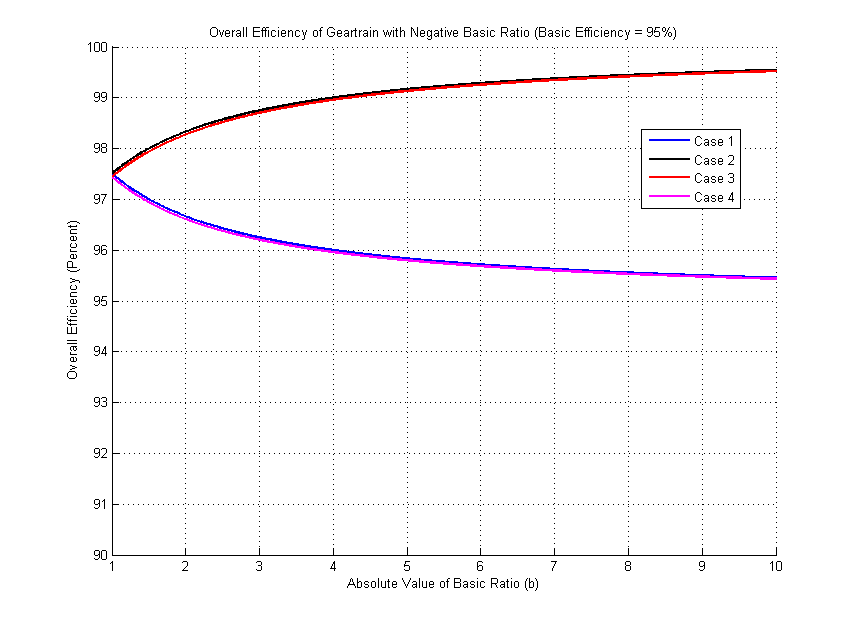
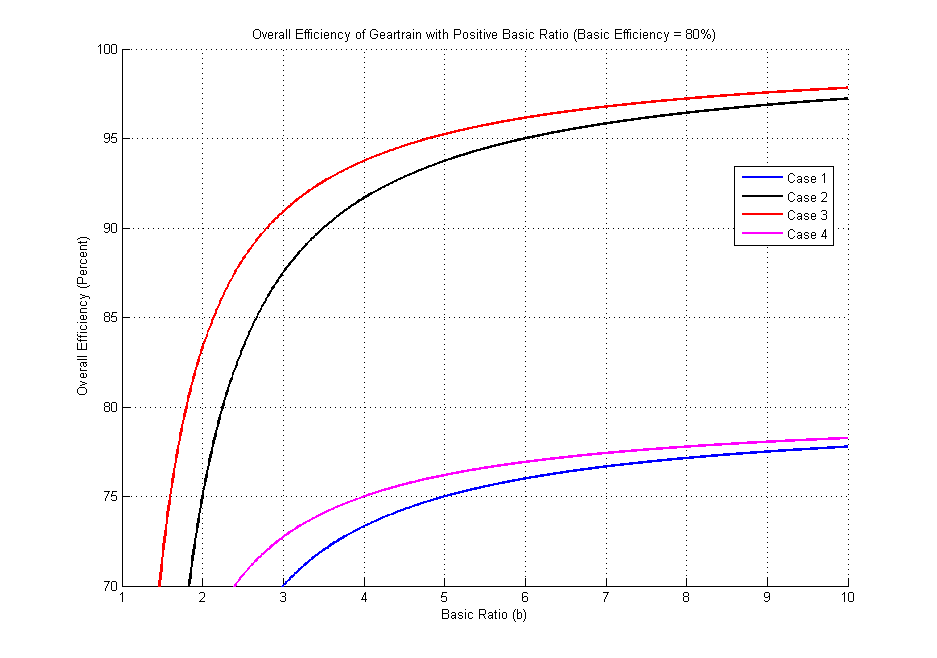
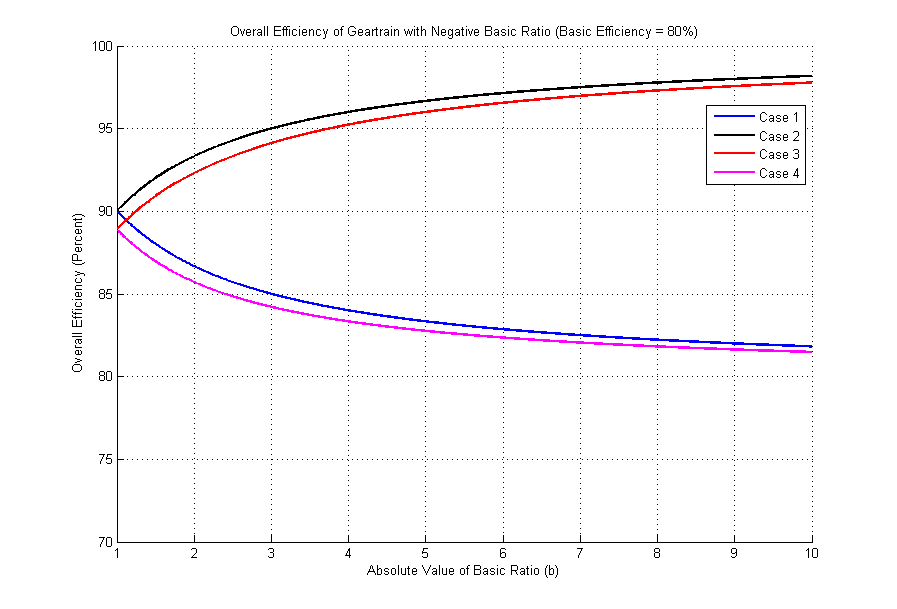
The overall efficiencies of planetary gearsets for various basic ratios are shown in the figures below. The first two show overall efficiencies with a basic efficiency of 95% and the second two show overall efficiencies if the basic efficiency is 80%. The vertical scales are different in the two sets of figures. One trend is evident in the figures: Cases 1 and 4 produce unacceptable low efficiencies for positive basic ratios and relatively low efficiencies for negative basic ratios. If the absolute value of the basic ratio must be close to 1, then a negative basic ratio will produce much better results than a positive basic ratio. It would seem that the designer should strive for Case 2 or 3 with a negative basic ratio in all cases, since these always have the highest efficiencies. In fact, Cases 2 and 3 do not permit large overall reductions (see the "Overall Ratio" column in the tables above), so we must usually compromise and use Cases 1 or 4 where large reductions are required.

[1] Merritt, H.E. Gear Engineering, John Wiley and Sons, 1972

[2] Molian, S. Mechanism Design: an Introductory Text, Cambridge University Press, 1982